Binary Tree - Traversal order - Post order, inorder, pre order traversal
Binary Tree is a tree in which each node can have at most two children.
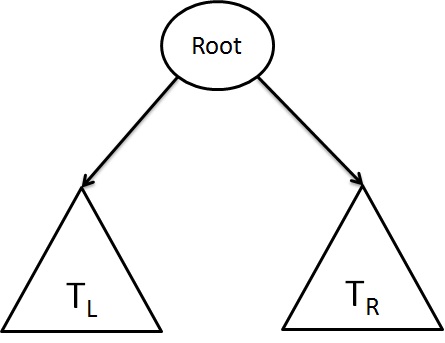
- Binary Tree consist of a root, two subtree TL and TR, possibly both of which could be empty.
- It is necessary to determine whether the tree is balanced by calculating the balance factor.
- The balance factor is defined as the difference in height between its left and right subtrees.
B = HL - HR
- The tree is balanced only if its balance factor is zero and its subtrees are also balanced.
Complete Binary Tree
A tree is considered complete tree if it has maximum number of entries for its height.
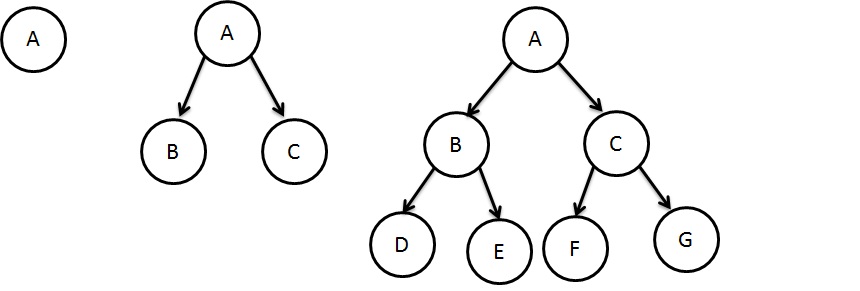
Nearly Complete Binary Tree
A tree is considered nearly complete tree if it has minimum number of entries for its height.
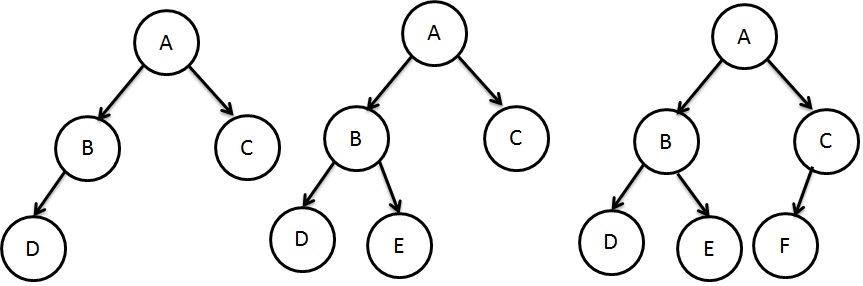
All the nodes in the last level are found on the left.
Binary Tree Traversal
Traversal is the process of visiting all the nodes in the tree exactly once. We have several approaches to traverse the tree that can be categorized into two approaches:
- Depth First Traversal
- Breadth First Traversal
Binary Tree - Depth First Traversal
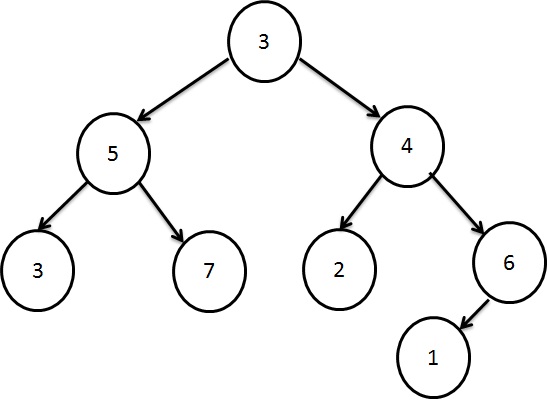
All the descendants of a child are processed before next child.
There are 3 types of depth first traversal:
In-Order Traversal
First visit left child; then root and then right child (Left-Root-Right. For the example tree above, traversal would be as shown below:
3 - 5 - 7 - 3 - 2 - 4 - 1 - 6
Pre-Order Traversal
first visit root; then left and right children. (Root-Left-Right). For the example tree above, traversal would be as shown below:
3 - 5 - 3 - 7 - 4 - 2 - 6 - 1
Post-Order Traversal
first visit left child and right child;then root. (Left-Right-Root). For the example tree above, traversal would be as shown below:
3 - 7 - 5 - 2 - 1 - 6 - 4 - 3
Binary Tree - Breadth First Traversal
- The processing starts horizontally from the root to all its children, then to its children's children, and so forth until all nodes have been processed.
- That means each level is completely processed before the next level is started
Let us consider the same example tree (Figure 4) the breadth-first traversal is:
3 - 5 - 4 - 3 - 7 - 2 - 6 - 1