Data Structures - Expression Tree
Next - Expression Tree Examples >>
Expression Tree is used to represent expressions.
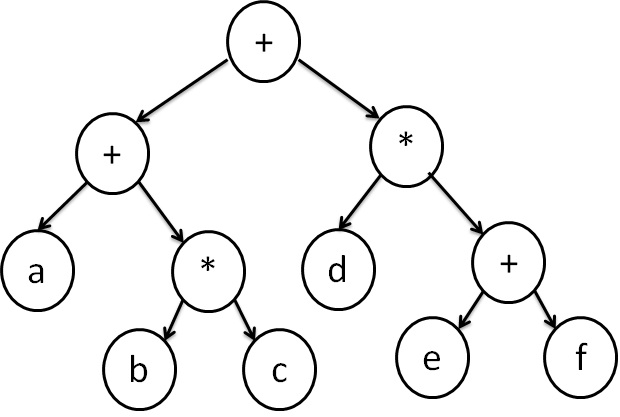
An expression and expression tree shown below
a + (b * c) + d * (e + f)
All the below are also expressions. Expressions may includes constants value as well as variables
a * 6 16 (a^2)+(b^2)+(2 * a * b) (a/b) + (c) m * (c ^ 2)It is quite common to use parenthesis in order to ensure correct evaluation of expression as shown above
There are different types of expression formats:
- Prefix expression
- Infix expression and
- Postfix expression
Expression Tree is a special kind of binary tree with the following properties:
- Each leaf is an operand. Examples: a, b, c, 6, 100
- The root and internal nodes are operators. Examples: +, -, *, /, ^
- Subtrees are subexpressions with the root being an operator.
Traversal Techniques
There are 3 standard traversal techniques to represent the 3 different expression formats.
Inorder Traversal
We can produce an infix expression by recursively printing out
- the left expression,
- the root, and
- the right expression.
Postorder Traversal
The postfix expression can be evaluated by recursively printing out
- the left expression,
- the right expression and
- then the root
Preorder Traversal
We can also evaluate prefix expression by recursively printing out:
- the root,
- the left expressoion and
- the right expression.
If we apply all these strategies to the sample tree above, the outputs are:
- Infix expression:
(a+(b*c))+(d*(e + f)) - Postfix Expression:
a b c * + d e f + * + - Prefix Expression:
+ + a * b c * d + e f
Construction of Expression Tree
Let us consider a postfix expression is given as an input for constructing an expression tree. Following are the step to construct an expression tree:
- Read one symbol at a time from the postfix expression.
- Check if the symbol is an operand or operator.
- If the symbol is an operand, create a one node tree and push a pointer onto a stack
- If the symbol is an operator, pop two pointers from the stack namely T1 & T2 and form a new tree with root as the operator, T1 & T2 as a left and right child
- A pointer to this new tree is pushed onto the stack
Thus, An expression is created or constructed by reading the symbols or numbers from the left. If operand, create a node. If operator, create a tree with operator as root and two pointers to left and right subtree
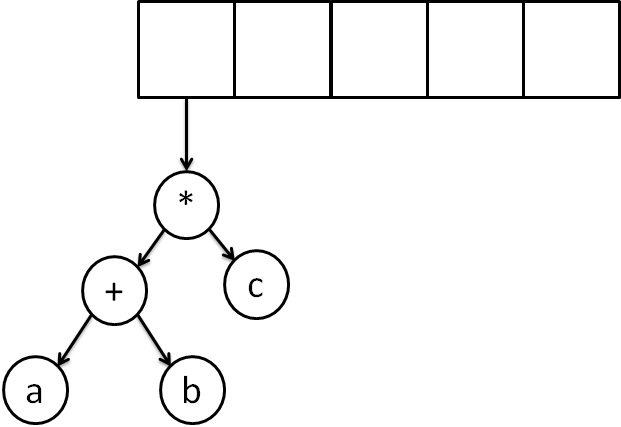
Example - Postfix Expression Construction
The input is:
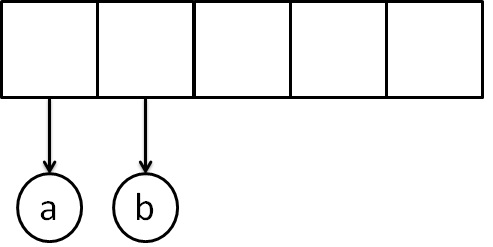
a b + c * The first two symbols are operands, we create one-node tree and push a pointer to them onto the stack.
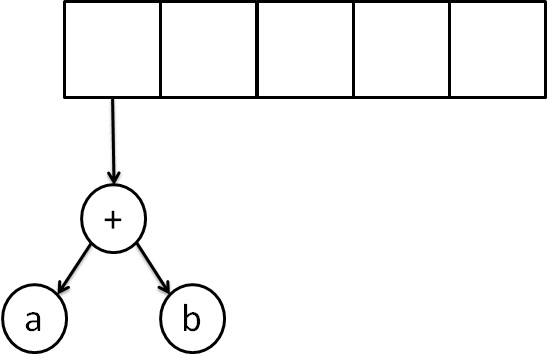
Next, read a'+' symbol, so two pointers to tree are popped,a new tree is formed and push a pointer to it onto the stack.
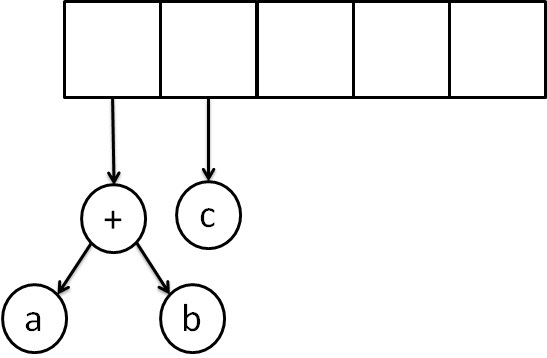
Next, 'c' is read, we create one node tree and push a pointer to it onto the stack.
Finally, the last symbol is read ' * ', we pop two tree pointers and form a new tree with a, ' * ' as root, and a pointer to the final tree remains on the stack.
Examples - How to Write Infix, Prefix, Postfix Expressions from Expression Tree >>
Next - Expression Tree Examples >>