Data Structures - Heap
Heap is binary tree structure that satisfies the two properties.
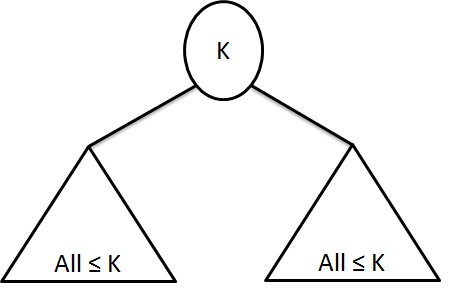
- The tree is complete or nearly complete - Structure Property
- The key value of each node is greater than or equal to the key value in each of its children -Heap Order Property
Heap has many uses
- To implement a priority queue.
- Used in sorting the data. Used in finding the shortest path. Used in finding the path with the minimum cost when each stage in the path has a cost associated with it
- To find the kth smallest or kth largest element in a group of elements
- Used in creating a minimum spanning tree
Minimum Spanning Tree created using a heap has many applications
- Used in Taxonomy for classification
- Used in Handwriting recognition and Data pattern recognition
- Feature selection when there are too many features and thus simplifying the model for easy understanding
- Used to describe relationship between two stocks in financial market
Structure Property
To better understand the structure of the heap. Let us examine the following heaps:
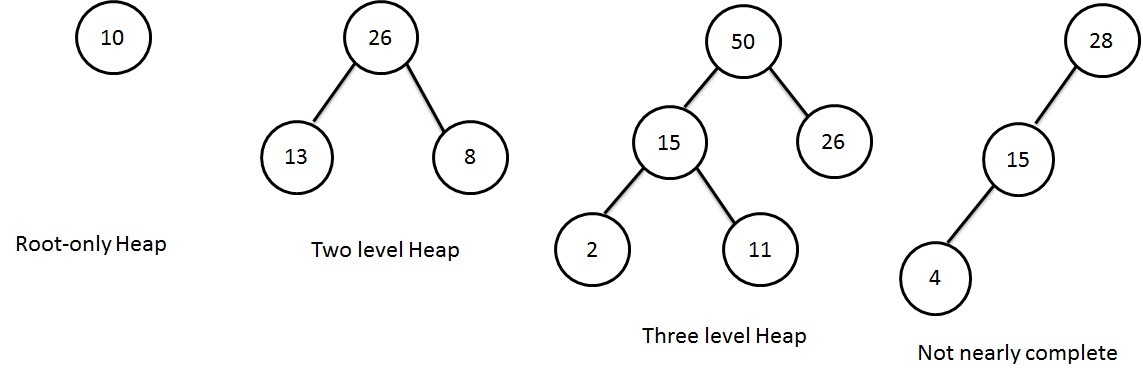
From the figure above:
- Root-Only heap: Root itself is considered as a binary heap.
- Two-level heap: it is a complete binary tree.
- Three-level heap: it is a nearly complete binary tree.
- The fourth tree is not a complete or nearly complete tree. Therefore it does not satisfy the structure property.
From this discussion we understand that, Heap is a complete binary tree, that is filled with the possible exception of bottom level, which is filled from left to right. This is called as complete binary tree.
The height of the complete binary tree is O(log n)
Heap Order Property
Heap order Property that allows operations to be performed quickly. In a heap, the key value of each node is smaller than or greater than the key value of parent with exception of the root because the root has no parent. Here there are two types of Heaps:
- Max-Heap
- Min-Heap
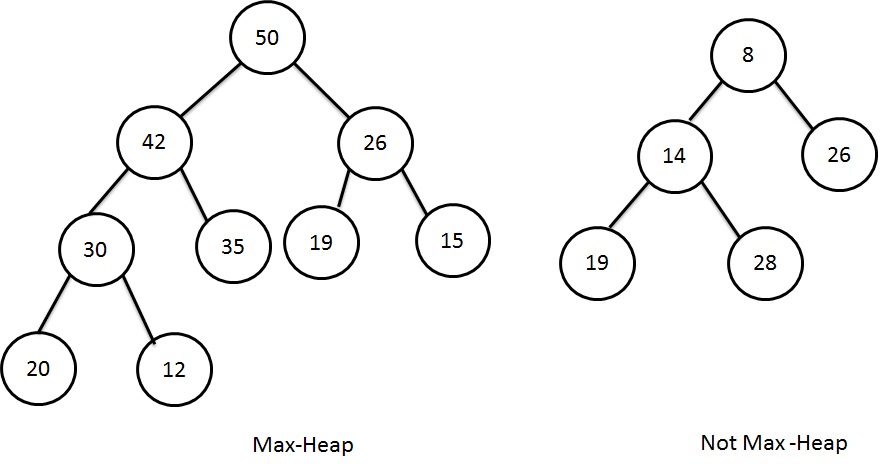
Max-Heap
For every node X, the key value in the parent of X is greater than the key value in the X (except root because root has no parent).
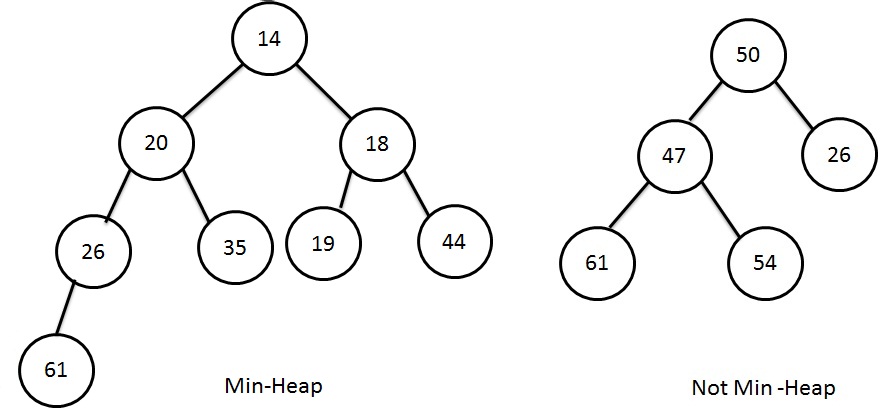
Min-Heap
For every node X, the key value in the parent of X is smaller than the key value in the X (except root because root has no parent).
Insert Operation
We are going to explain how to insert an element into the Min-heap. The following is the procedure for insertion of an element into Min-heap.- Create the new node in the next available location.
- Insert the new value into the new node.
- Check whether the new node can satisfy the heap order property. That means, for min-heap, value of parent node is smaller than the child node.
- If it does not affect the heap order, then that insertion is successful.
- If it affects the heap order, then do the swapping the parent with child node.
- Continue this process until the new element can be placed in the correct location.
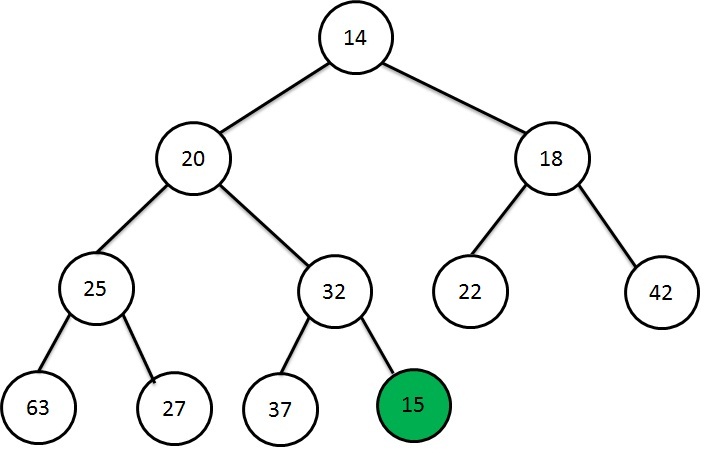
Check if the 15 is greater than 32. if it is not, then 15 is pushed up as it is smaller than parent node. Now 32 becomes the child of 15
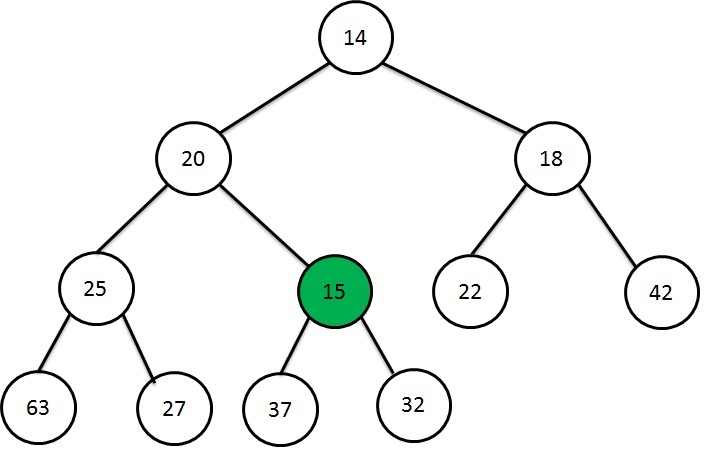
Still the 15 cannot be inserted, since it is smaller than its parent node. So we again need to swap them. Now the node 20 will become the right child of node 15.
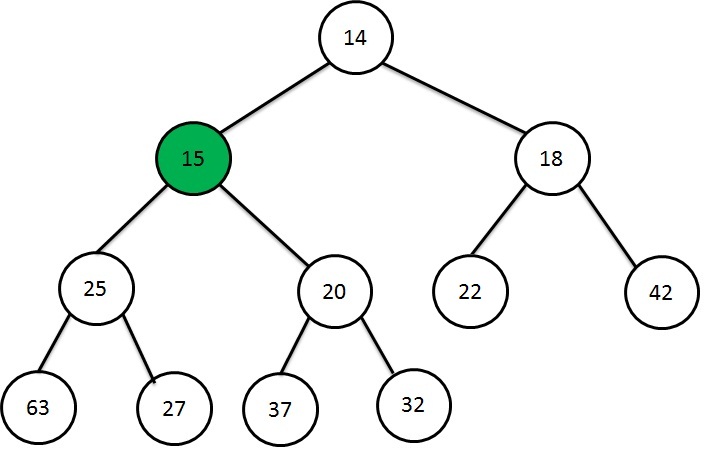
Now the 15 has been inserted in the correct location which also satisfy the heap order.
This entire process is known as Precolate up (or) Reheap up. That means, a new element is precolated up to the correct location. The insertion of new element into the heap requires O(log n) time. The process of insertion to Max-heap is similar to that of Min-heap but only one difference is that the value of parent node is always greater than the child node.
Deletion
We can see how to delete the minimum element from the heap. In Min-heap,the minimum value is found at the root which can be removed easily but it is very complicated to restore the keep order property.
The following is the procedure for deleting minimum value:
- First remove the root node, at which the minimum value is found, and replace it with last element of the heap.
- Next restore the heap order property is that the parent value is less than their children values.
- If it does not satisfy the heap order property, then we need to swap the root with its smallest child node
- Repeat this swapping of node with their children until the node can be placed in the correct location.
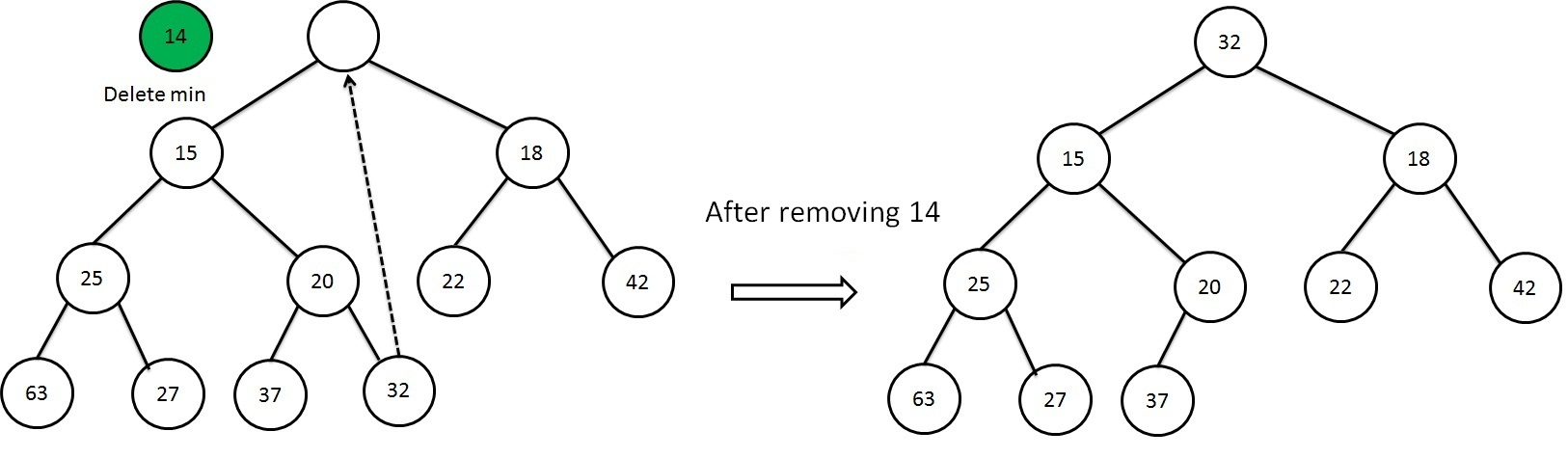
The root has been violating the heap order. In order to maintain heap order, we need to swap the parent node with smallest value of their child node.
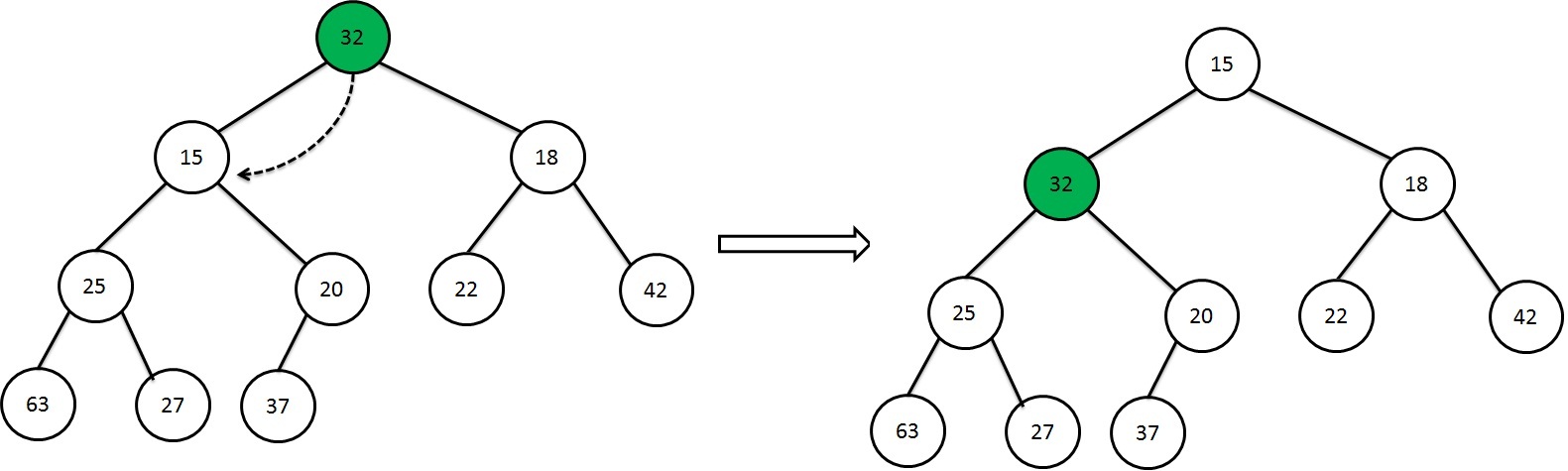
Still the property has violated, so again we swap the left subtree with their smallest child node.
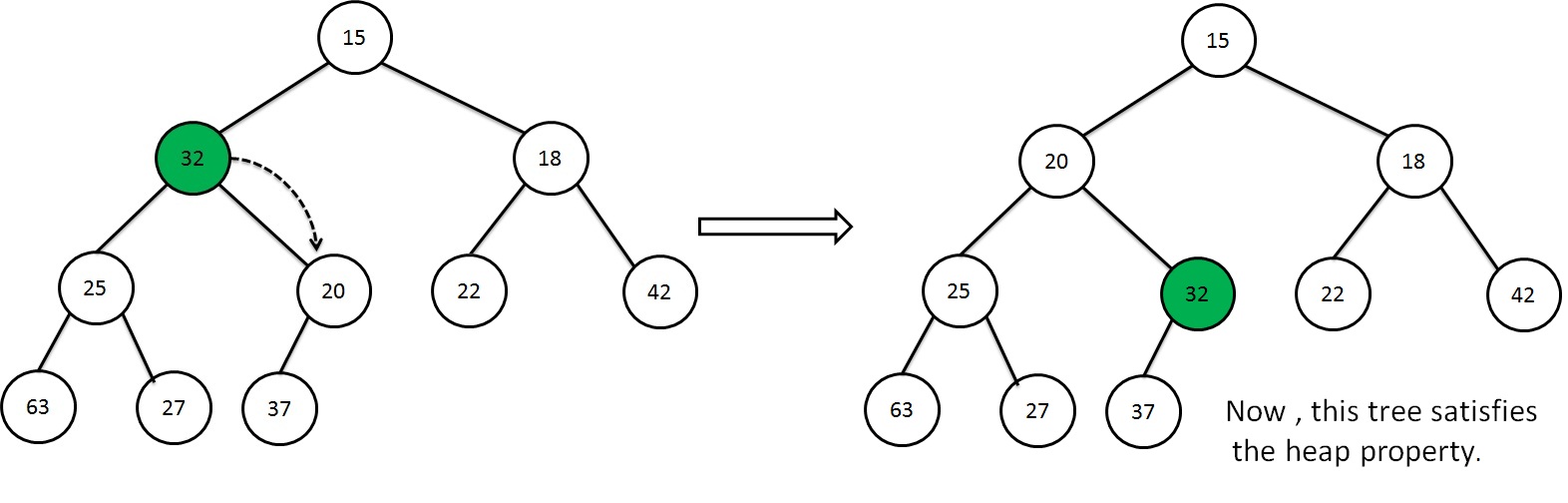
This process is called as Precolate down (or)Reheap down. The average running time required for this operation is O(log n)