We are following the decimal numbering system in our day to day calculation. This system has ten digits so that it is called the base 10 number system. The computer can not directly use this decimal number for any mathematical calculations. Because the computer can understand only 0's and 1's. Here, there are the steps to convert this decimal into other number systems that follow.
- Step 1:
Divide the given decimal with a corresponding base value like base 2, base 8, and base 16. then note down the quotient and remainder.
- Step 2:
Next, again divide the resulting quotient with the corresponding base value and keep a note on quotients and remainders. This process will be continuing until the quotient is zero.
- Step 3
Now write all the remainder in reverse order. The first remainder is the least significant digit, and the last reminder is the most significant digit.
In the case of the fractional part of a decimal number, the following are the steps considered to convert it into other number systems.
- Step 1:
In the first step, multiply the fractional part of decimal with corresponding base value such as 2, 8, and 16 and note down the result and carry.
- Step 2:
Next, multiplying the result from the first step with the corresponding base value and keep a note on results and carries. The process will be continuing until the result is zero.
- Step 3:
Now write the normal sequence of carries(from top to bottom) that is the equivalent fractional part of the other number systems.
Decimal to Binary
for example: convert the decimal (162.75)10 into a binary number.
Step 1:
Divide the integer part of the decimal number 162 and its consecutive quotients with base 2 and keep on note down the remainders until the quotient is zero
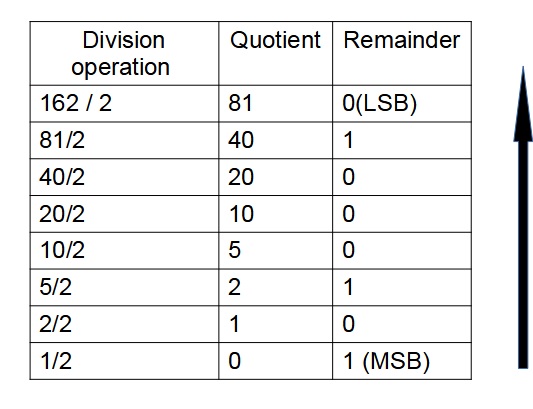
The equivalent binary number for the decimal(162)10 is (10100010)2
Step 2:Multiply the fractional part of the decimal number (0.75)10 and its consecutive results with base 2 and keep on note down the carries until the result is zero.
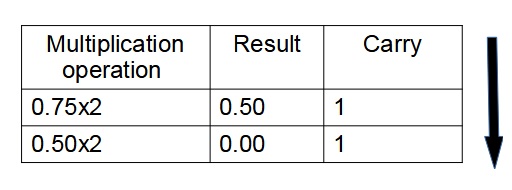
The equivalent binary number for the fraction part of the decimal(0.75)10is (0.11)2
Therefore,the decimal nember (162.75)10 = (10100010.11)2 binary number
Decimal to Octal
For example: convert the decimal (162.75)10 into a octal number.
Step 1:
Divide the integer part of the decimal number 162 and its consecutive quotients with base 8 and keep on note down the remainders until the quotient is zero
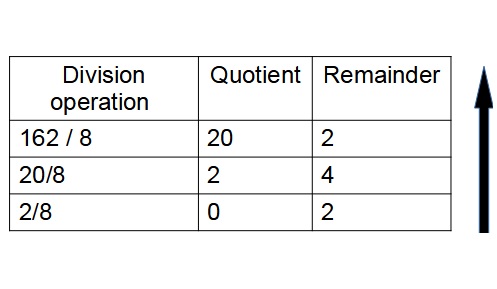
The equivalent octal number for the decimal(162)10 is (242)8
Step 2:Multiply the fractional part of the decimal number (0.75)10 and its consecutive results with base 8 and keep on note down the carries until the result is zero.
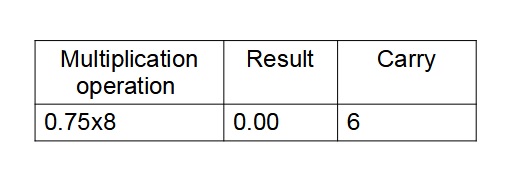
The equivalent octal number for the decimal(0.75)10 is (0.6)8
Therefore,the decimal nember (162.75)10 = (242.6)8 octal number
Decimal to Hexadecimal
for example: convert the decimal (162.75)10 into a hexadecimal number.
Step 1:
Divide the integer part of the decimal number 162 and its consecutive quotients with base 16 and keep on note down the remainders until the quotient is zero
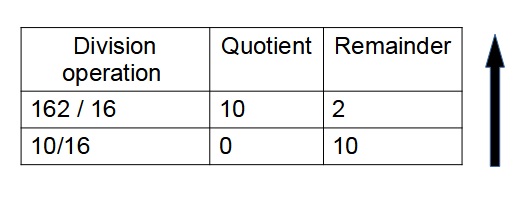
The equivalent hexadecimal number for the decimal(162)10 is (A2)16
Step 2:Multiply the fractional part of the decimal number (0.75)10 and its consecutive results with base 16 and keep on note down the carries until the result is zero.
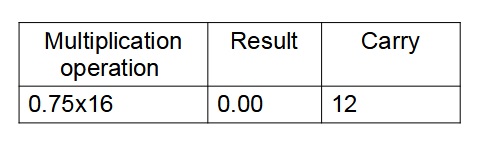
The equivalent hexadecimal number for the decimal(0.75)10 is (0.C)16
Therefore,the decimal nember (162.75)10 = (A2.C)16 hexadecimal number








