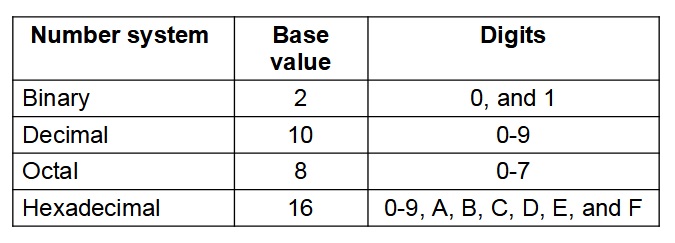
Computers can understand only 0s and 1s. Any alphabets like A, a or numbers like 1 or 2 or special characters like " or # or % is represented in terms of 0s and 1s. These techniques used to represent characters or numbers in a computer system are called number system. Various number systems available for our use are:
- Binary
- Decimal
- Hexadecimal
- Octal
- Number
Number is a symbol to represent a unit.
- Number system
Number System defines the set of symbols/digits used to represent the unit.
- Radix or Base
Base is the number of digits available for that particular number system.
Binary Number System
Binary number system uses only two digits, 0 and 1, to represent data. Each digit in a binary number is called a bit. A group of eight bits is called one byte. A group of four bits is called a nibble. If you enter any data into the computer that can be converted into electrical signals so that the 0 represents the absence of an electrical signal whereas 1 represents the presence of an electrical signal. Hence, it is known as the base 2 number system. Each digit represents the positional value that is expressed in the power of base 2. In a binary number, there are 2 important positions that are the least significant bit (LSB) or the right most digit and the most significant bit (MSB) or the left most digit.
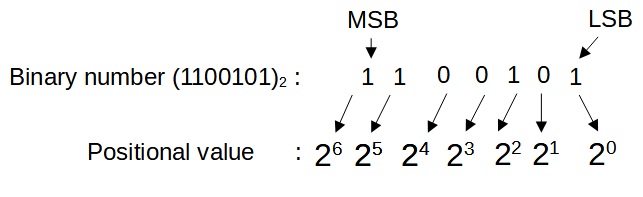
Example of binary numbers: (1011)2 , (111)B , (1001)B , and (10111.110)2
Decimal Number System
Decimal number system consists of ten digits 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. So. this number system is known as the base 10 number system. Each digit from right to left of the decimal number is represented as units, tens, hundreds, thousands, ten thousands, and so on. We use this number system for our daily calculations. The positioning of each digit is denoted as a power of base 10. Numerical value in the decimal number system is determined by multiplying each digit of the decimal number with the corresponding positional value and then adding all the products.

Example of decimal numbers: (25)10 , (1005)10 , and (156.90)10
Octal Number System
Decimal Number System consists of 8 numerical digits from 0 to 7. So, it becomes base-8 number system using the digits 0, 1, 2, 3, 4, 5, 6 and 7. Positional value of each digit in this number is represented as a power of base 8. A group of 3 bits of a binary number can be used to represents each digit in an octal number.

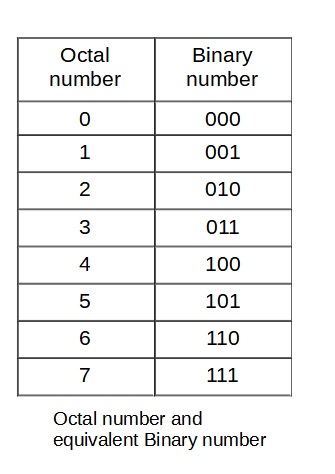
Example of octal numbers: (25)8 , (16)8 , and (40)8
Hexadecimal Number System
Hexadecimal number system uses 10 decimal numbers and 6 Alphabets. So, it is known as the base 16 number system. The numbers are 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E and F. The positional value of each digit is represented as a power of 16. Each group of 4 bits of a binary number can be used to represent each digit in a hexadecimal number.

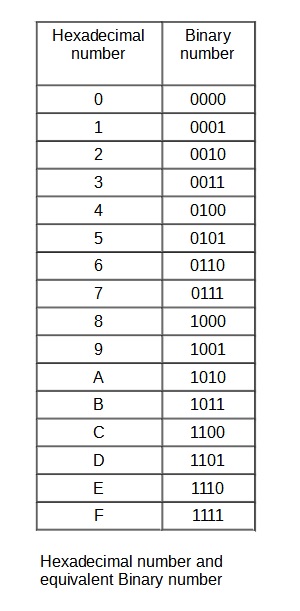
Example of hexadecimal numbers: (20)16 , (AC)16 , and (28)H or (28)16
Summary of Number System