Why do we need number system conversions?
Computer is an electronic or digital device that operates based on an on /off switch.
1 represents ON, and 0 represents OFF.
The two digits 0 and 1 are called binary numbers.
Computer can understand only the two binary numbers (0s and 1s).
- As humans, we use the decimal number system in our day to day life.
- For computers, every decimal number and instruction has to be converted into a binary number.
- For large decimal number, the binary representation is too long that is very difficult for the user to interpret.
- To simplify usage and interpretation, the octal and hexadecimal numbering systems are used.
A group of four bits of the binary number is equal to one digit of a hexadecimal number
A group of three bits of the binary number is equal to one digit of the octal number.
Long numbers are less lengthy in hexadecimal system. Hence, Hexadecimal numbers are used more than the octal numbers. Octal is still utilized in a few scenarios.
For easy reading and understanding, the programmer can often use a hexadecimal numbering system. Nowadays, most computers are designed to process the hexadecimal numbers.
4 numbering systems available for our use on which each one can be converted to other three number systems. The possible number system conversions are
- Binary number to Decimal / Octal / HexaDecimal number conversion
- Decimal to other number system conversion (Binary, Octal, and Hexadecimal)
- Octal to other number system conversion (Binary, Decimal, and Hexadecimal)
- Hexadecimal to other number system conversion (Binary, Decimal, and Octal)
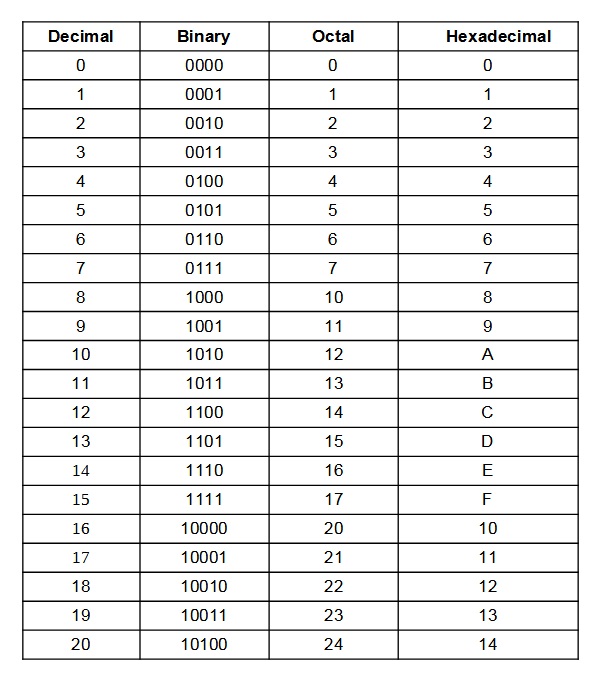
Following table shows the Decimal, Binary, Octal, and Hexadecimal equivalents:
| Decimal | Binary | Octal | Hexa Decimal |
|---|---|---|---|
| Base 10 | Base 2 | Base 8 | Base 16 |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| Decimal | Binary | Octal | Hexa Decimal |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| Decimal | Binary | Octal | Hexa Decimal |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
| Decimal | Binary | Octal | Hexa Decimal |
| 16 | 1 0000 | 20 | 10 |
| 17 | 1 0001 | 21 | 11 |
| 18 | 1 0010 | 22 | 12 |
| 19 | 1 0011 | 23 | 13 |
| 20 | 1 0100 | 24 | 14 |
| Decimal | Binary | Octal | Hexa Decimal |
| 21 | 1 0101 | 25 | 15 |
| 22 | 1 0110 | 26 | 16 |
| 23 | 1 0111 | 27 | 17 |
| 24 | 1 1000 | 30 | 18 |
| 25 | 1 1001 | 31 | 19 |
| 26 | 1 1010 | 32 | 1A |
| Decimal | Binary | Octal | Hexa Decimal |