Let us learn about what is a AVL tree, about AVL tree rotation, AVL tree insertion with AVL tree examples
AVL Tree - Binary Tree with Balance condition
AVL tree full form, named from their inventors, Adelson, Velskii & Landis tree is binary search tree with a balance condition. The balance condition is determined by the difference between the heights of subtrees of the root in the tree.
- AVL tree ensures that Insertion, Deletion and Search operations take
O(log n)in both average and worst cases. - AVL tree is a balanced binary search tree in which the height of left and right subtrees differ by no more than one.
Why AVL Tree?
Let us consider the 2 scenarios that are given below. Both have the same elements arranged in 2 different ways.
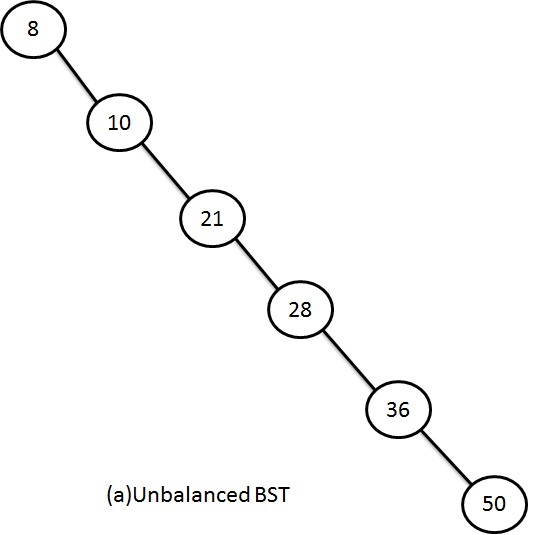
Unbalanced Binary Search Tree
When we consider case (a) - the Unbalanced Binary Search Tree:
- If we want to locate 10, it will require 2 tests. That is checking whether the first node is 10 and then checking whether the second node is 10.
- If we want to locate 50, it requires 6 tests checking each node until you find 50
- Hence, the maximum search effort for this tree data structure is equal to the number of elements in the tree, otherwise called as Order of n, or simply represented as O(n).
- Thus performance in the worst case scenario, is closer to the sequential search algorithms such as List.
- In order to make searches faster, we need to balance the unbalanced Binary Search tree (BST).

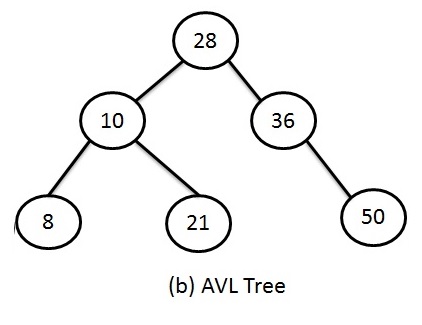
AVL tree - balanced Binary Search Tree
Now consider the case (b) - AVL tree:
- If we want to locate a value which is far from the root, say 8, we start by comparing with the root value 28.
- Since 8 < 28, then we next search the left subtree node and compare 8 with 10.
- Since 8 < 10, then we search the left subtree node 8.
- Since 8 is found, this search needs only 3 tests.
- So the maximum search effort for this tree is O(log n).
- When we compare these 2 samples, we see that even in the worst case scenario, search effort was reduced from 6 to 3.
AVL Tree - Balance Factor
AVL tree is a binary search tree that is either empty or that consists of two AVL subtrees, Left subtree TL and right subtree TR whose heights differ by ≤1. This height difference is called Balance Factor. Balance factor for any node in AVL tree must be +1, 0, (or)-1.
|HL-HR| < = 1
Where HL and HR are the height of left and right subtree respectively. AVL tree is also called height-balanced binary search tree.
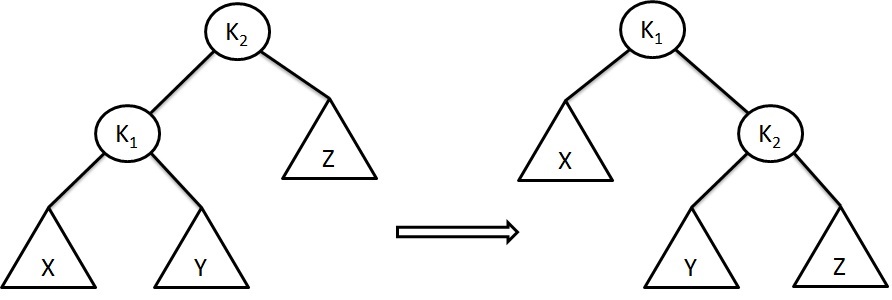
AVL Rotations
Whenever we insert a node into a tree (or) delete a node from a tree, the resulting tree may be unbalanced. We must rebalance this unbalanced tree. The balancing of AVL tree is done by rotating the node either to the left or to the right.
There are two kinds of Rotations:
- Single Rotation
- Double Rotation
All unbalanced AVL trees fall into 1 of these 4 cases:
- Left of Left
- Right of Right
- Right of Left
- Left of Right
In the first 2 cases, insertion occur on the "Outside". This is fixed by single rotation. Whereas in cases 3 & 4, insertion occurs on the "Inside". This is fixed by double rotation. Let us discuss these scenarios one by one.
AVL tree - Left of Left
If the AVL tree becomes unbalanced, because of insertion into the left subtree of left child, then we rotate the out-of-balance node to the right.
Let us consider an example below:
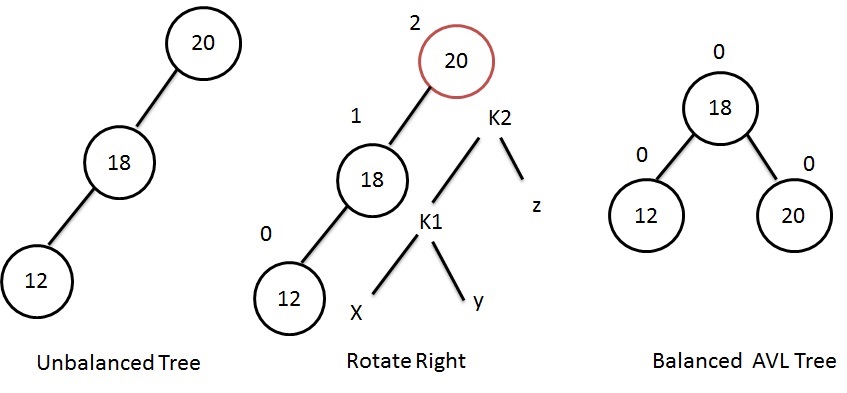
In the example above, the out-of-balance condition has been created by inserting node 12 on its left child of left. Here, we must rebalance the tree by rotating out-of-balance node 20 to the right.
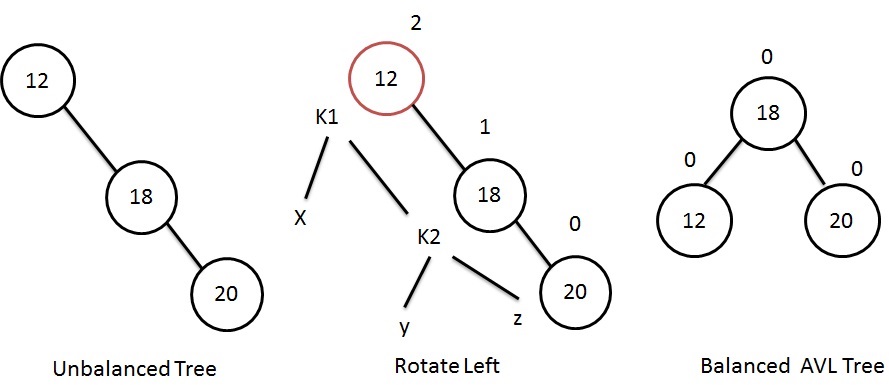
AVL tree - Right of Right
If the AVL tree becomes unbalanced, due to the insertion into the right subtree of the right child, then we need to rotate the out-of-balance node to the left.
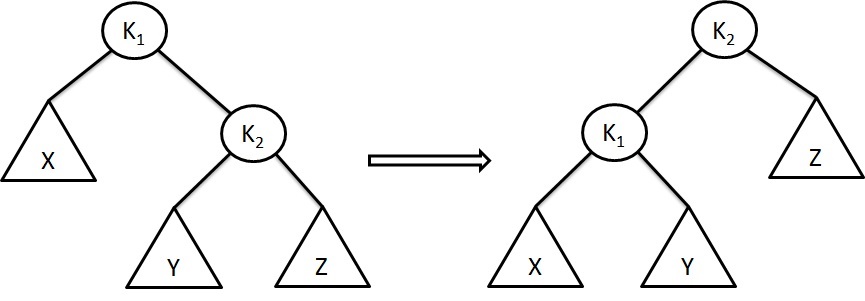
An Example:
It is opposite to that of Left-of-Left. Let us say, we find an out-of-balance after inserting a node to the right. In this case, we must rebalance the tree by rotating the out-of-balance node to the left. In our example, inserting of node 20 will cause the out-of-balance at node 12, so we need to rotate that node 12 to left, in order to bring the tree to in-balance condition.
AVL tree - Right of Left
Double rotation is similar to single rotation but involves 4 subtrees instead of 3. Here, we study 2 out-of-balance conditions in which we need to rotate the 2 nodes. Let us discuss right-of-left case. In right-of-left, the out-of-balance caused by inserting into the right subtree of left child. We need to balance the tree by rotating the right subtree to right and root to left.
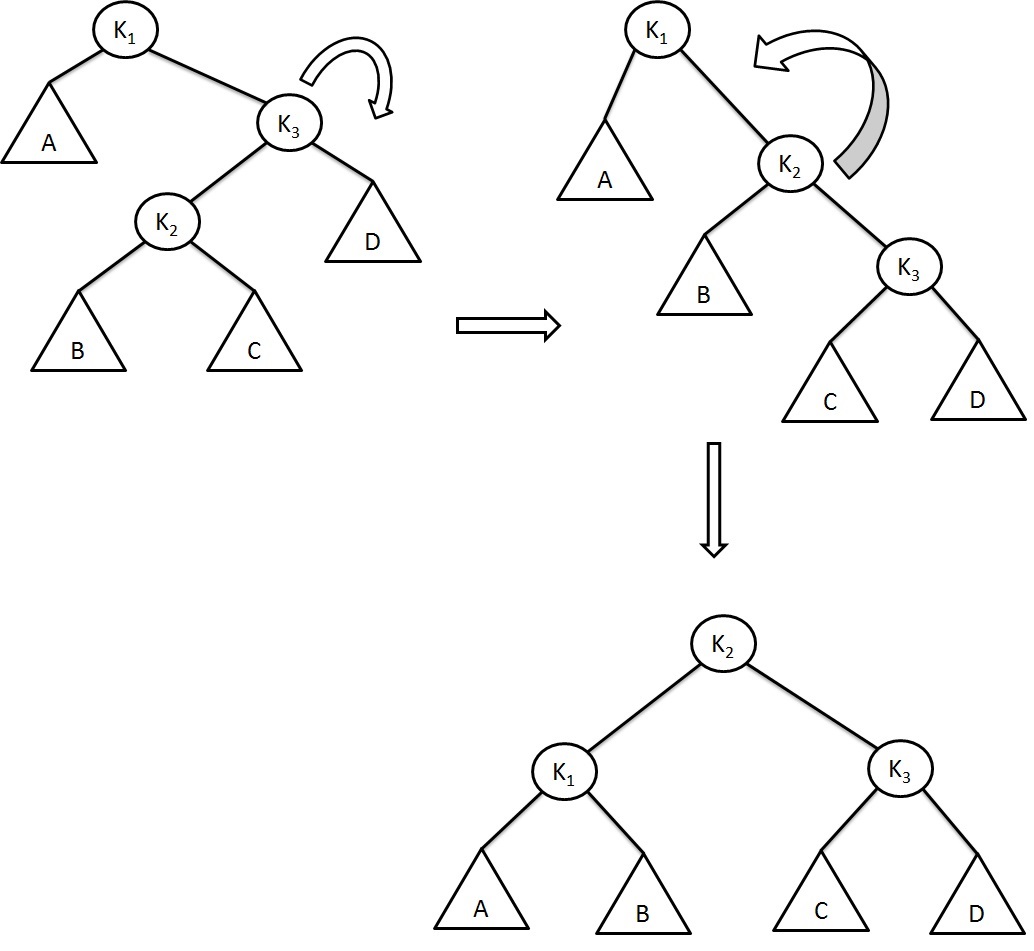
Let uss explain this AVL tree rotation Right-of-Left case with given example:
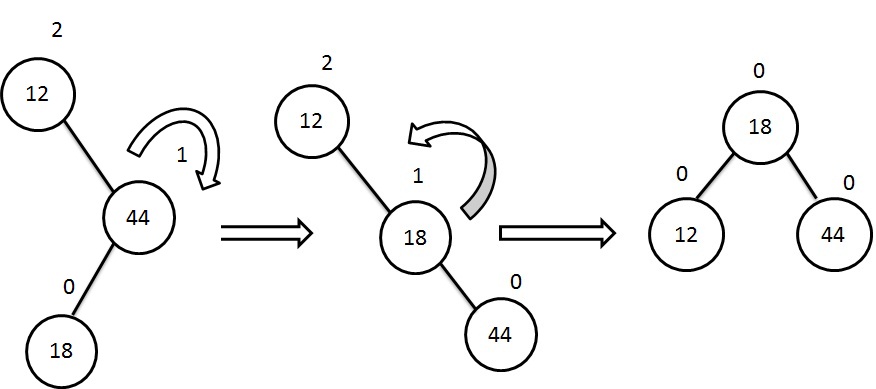
In the example above, the node 18 is inserted on left of right-subtree. This will make node 12 in unbalanced condition. It is necessary to balance it by rotating node 44 to right, making 18 as a right subtree of root node 12. Now, the node 12 is still unbalanced, so we need to perform the second rotation. That means, rotate the root-node to left and making the node 12 as a left subtree of node 18.
AVL tree - Left of Right
It is opposite to that of Right of Left case. To balance the tree, we first rotate the left subtree to left, then we rotate the root to the right and making the left node as the new root.
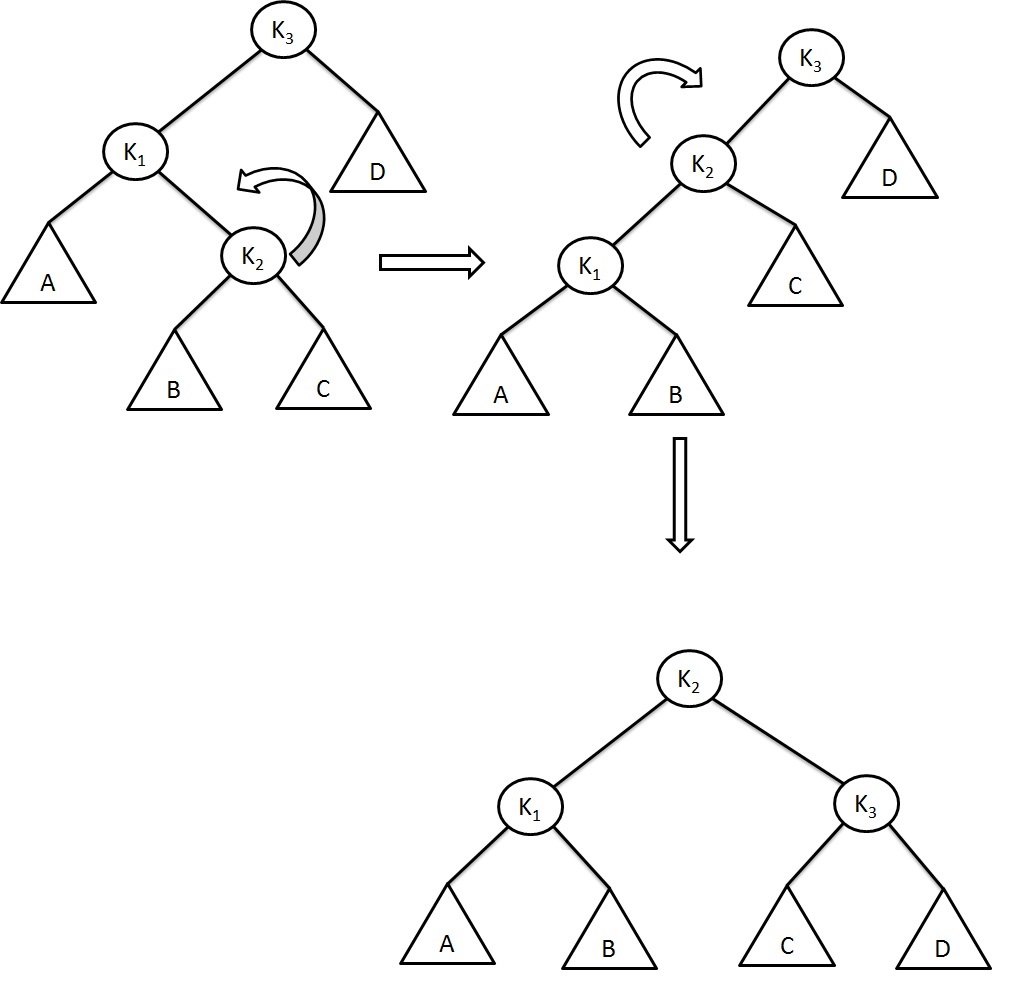
AVL Tree Rotation Example
Let us explain this AVL tree rotation Left of Right case with given example:
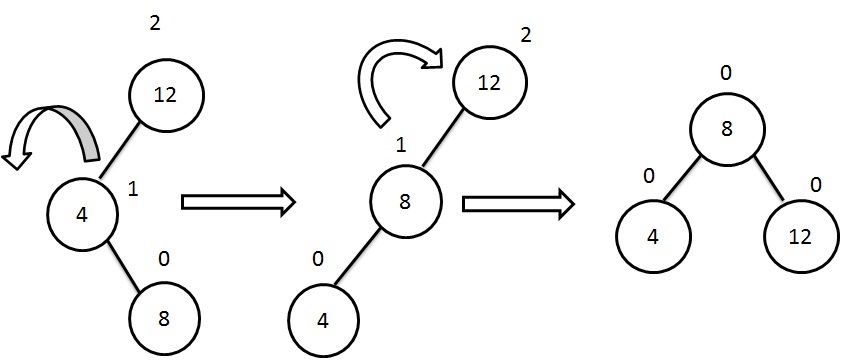
In the AVL tree example above, the node 8 is inserted on right of left subtree. So the node 12 is unbalanced. To balance it by rotating node 4 to left and making node 8 as the left subtree of root node. Now we again check the balance condition, still root node is unbalaced. So, we shall do the second rotation by rotating the root node to right. Finally we will get the balanced tree.






