Tree Data Structure - ADT
Tree is a data structure better understood visualizing it in the shape of a tree having a root, branches, sub branches and leaves.
If you draw the tree data structure, you draw the tree upside down with the root at top, branching out and having leaves at the sides and bottom of the tree.
A tree will have one and only one root node.
If you consider a tree has n nodes, it would have n-1 edges. Every node has one parent node except the root node.
Tree is a simple and more useful data structure in which the average running time of most operation is O(log n).
Tree data structure is useful in a number of scenarios or use cases
- Tree data structure is used to implement the file system of computer system. For example, like Windows explorer on Windows OS, File Manager on Android mobile phones, Files software on some Linux operating systems
- Tree data structure is used to evaluate simple or complex mathematical expressions. This kind of tree is a special tree called the
- Tree data structure supports searching operations in O(log n) average time.
Binary tree and ternary tree support search operations
Tree data structure consists of a finite set of elements(called nodes) and a finite set of directed line (called branches or edges)
Terminology used in Tree Data Structure
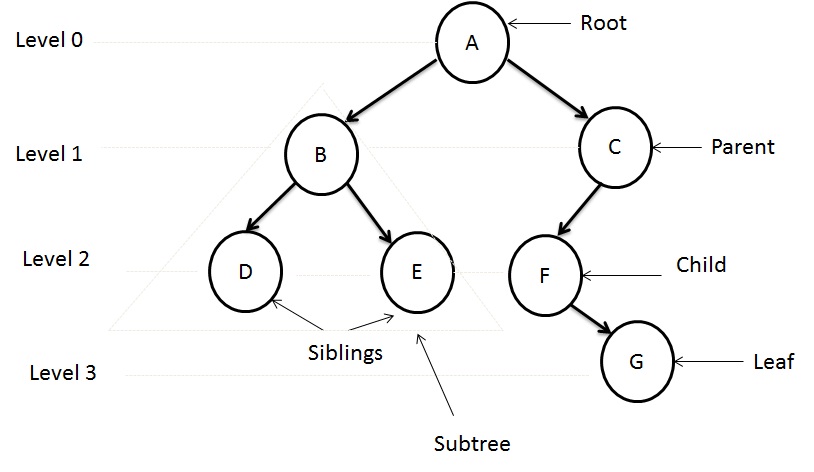
Various terms are used to describe the attributes of a tree as given below. These terms have been described based on Figure 2
- Root
- The first node is called root, in which indegree of root is zero. Root node is A
- Subtree
- It is the connected structure below the root node.
- Leaf
- Leaf is any node in which outdegree of the node is zero. Leaf nodes are D, E, and G
- Parent
- A node is parent if it has successor nodes. Parent nodes are B, C, and F
- Child
- The node is a child if it has a one predecessor. B and C are the Child nodes of A.
- Siblings
- Two or more nodes with same parent. D and E are siblings
- Ancestor
- It is any node in the path from root to that node. The ancestors of node D are B and A
- Descendant
- All the nodes in the path from a given node to a leaf node. The descendents of node C are F and G
- Path
- It is a sequence of nodes in which each node is adjacent to the next one. For reaching D, AB and BD these two branches should be added. Path is ABD
- Degree
- The number of lines associated with a node is called degree of the node. Degree of node B = 3
- Degree of the node = Indegree + Outdegree
- Indegree
- Number of branches directed towards the node. Indegree of node B = 1
- Outdegree
- The branch is directed away from the node. Outdegree of node B = 2
- Level
- It is a distance from root node is that root node is at level 0, its next child is at level 1, and its grandchild is at level 2 and so on.
- Level 0 node A
- Level 1 nodes B and C
- Level 2 nodes D, E and F
- Height of the tree
- The height of the tree is the level of the leaf in the longest path from root plus one.
- The height of the tree is 4 (i.e. it has 3 levels (3+1))
- Length of the path
- It is the number of edges on that path. The length of the path from A to F is 2
- Depth
- The depth of the node is the length of unique path from root to that specific node. The depth of node G is 3
- Height of the node
- The height of the node is the longest path from that node to leaf. The height of node C is 2







