Separate Chaining or Open hashing

<<Previous - Hashing Collision

Next - Closed Hashing>>

Open Hashing alias Separate Chaining

Open Hashing or Separate Chaining method maintains a list of all values that are hashed to the same location. In this method, the hash data structure is slightly modified. Instead of storing the value in an array, hash table in open hashing uses a linked list. Values will be stored in the linked list. For ease of use, the Linked list has a header. Each index of an array points to one element of the linked list. Assume a value is inserted into the hash table. It is added to the linked list at the corresponding index in the array. Hence, the collisions no longer happen since a linked list has no limit on its length. If more than one key point to the same array index, all the keys will be added to the linked list.

Open Hashing or Separate Chaining Example

Let us say that we have a sequence of numbers { 437, 325, 175, 199, 171, 189, 127, 509} and a hash function H(X) = X mod 10 Let us see the results of separate chaining hash table.

Separate Chaining Solution:

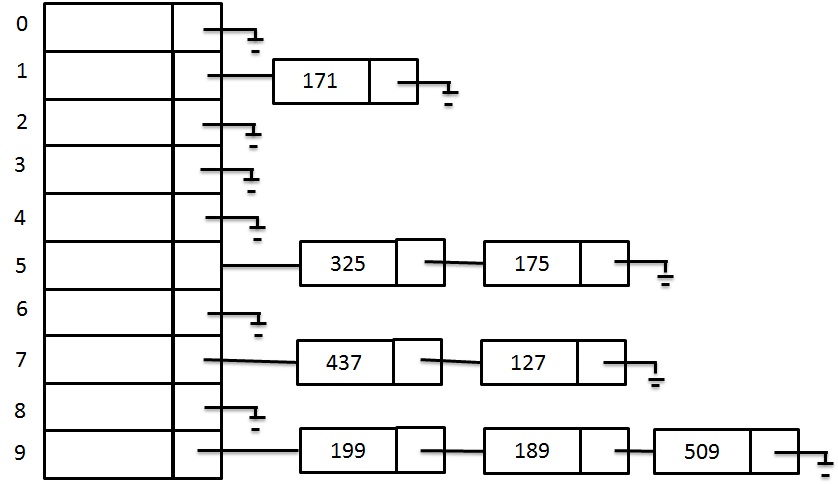
 For first key: 437
      		H (437) = 437 % 10 = 7
  		The index for 437 is 7.
 For key: 325
                H (325) = 325 % 10 = 5
                The index for 325 is 5.
 For key: 175
                H (175) = 175 % 10 = 5
                The index for 175 is 5.
 For key: 199
 		H (199) = 199 % 10 = 9
 		The index for 199 is 9.
 For key: 171
 		H (171) = 171 % 10 = 1
 		The index for 171 is 1.
 For key: 189
                H (189) = 189 % 10 = 9
                The index for 189 is 9.
 For key: 127
               H (127) = 127 % 10 = 7
               The index for 127 is =7.
 For key: 509
               H (509) = 509 % 10 = 9
               The index for 509 is 9.
 

Searching using Hashing

If you want to search a data, first we calculate an index by using hashing and then go to that location in the array and look down the list. There you see if that data is present in the list. The constant time required for this sear is O(1). For worst case, When every elements hashed to same location, in that we would be really doing a straight linear search on the linked list, which means that the time required to search an element is O(n).

Open Hashing or Separate Chaining - Disadvantages

• Open Hashing requires pointer and this may slow down the process of inserting of an element into the table.
• Open Hashing also needs the extra memory for linked list data structure.

To overcome the disadvantages, an alternative method Closed Chaining can be used to avoid the collision. Let us see that next.

<<Previous - Hashing Collision

Next - Closed Hashing>>