Dijkstras Algorithms or Algoritm for Shortest Path example

Dijkstra's Algorithm - Shortest Path First Algorithm

Dijkstra's algorithm used to solve single source shortest path problem. It follows a Greedy Algorithm. Generally greedy algorithm solves a problem in stages and it finds the solution that appears to be the optimum solution at each stage. The Dijkstra's algorithm proceeds in stage. At each stage, it finds the shortest path from source to every other vertex. For doing this, we will keep track of three pieces of information for each vertex such as

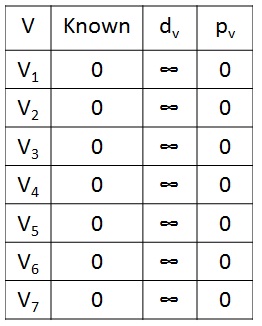
Known = set to 1 for a vertex after it is processed. Initially all vertices are not known.
d_v = keeps distance of the vertex from source s. Initially all vertices are ∞ except source s.
p_v = book keeping variable, used to print actual path.

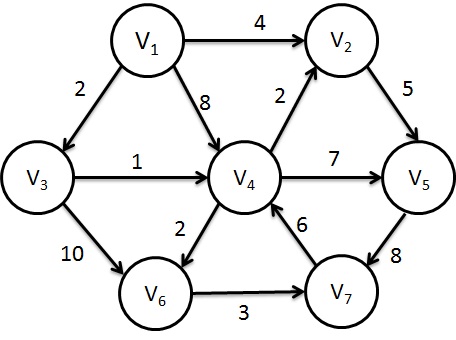
Fig 1. Example Graph with initial configuration table

Dijkstra's Algorithm - Steps to find the shortest path

Initially cost associated with none of the vertices are known. So the entry in "known" value for a vertex is 0, d_v is ∞ and p_v is 0.
Select the source vertex 's' and set the known entry to '1'
Update the distance value of all adjacent vertices of the source vertex s by using
d_w=d_v + C_{v, w}
where C_{v, w} is the cost or weight on the edge of the adjacent vertex.
Next, pick up the vertex V who has the smallest distance d_v among all the unknown vertices.
Then declare that the shortest path from s to v is known. Again update the distance value d_v of all the adjacent vertices of v by using d_w=d_v + C_{v, w}.
If the new value d_w is greater than the old one, then we simply ignore that value otherwise we will insert the new value into the d_v entry.
Repeat the steps 3, 4 and 5 until all vertices are known.

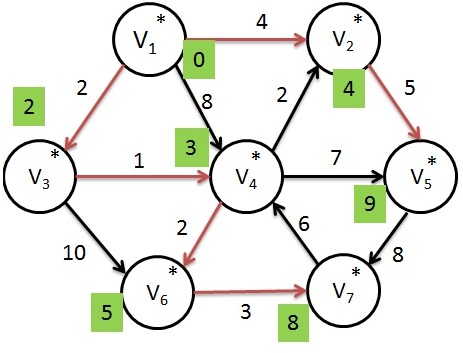
Dijkstras Algorithm - Finding Shortest path for Above Graph

Let us consider the above graph, now we want to find the shortest path from source to all other vertices using Dijkstra's algorithm.

Dijkstras Algorithm - Step 1

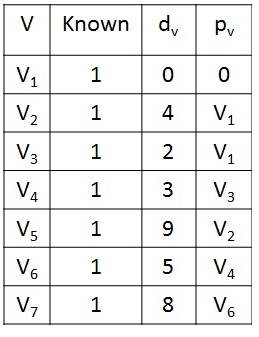
First, we select the source vertex as V₁, with path length 0 and we set known value to 1 and update the distance value of adjacent vertices such as V₂, V₃, and V₄.

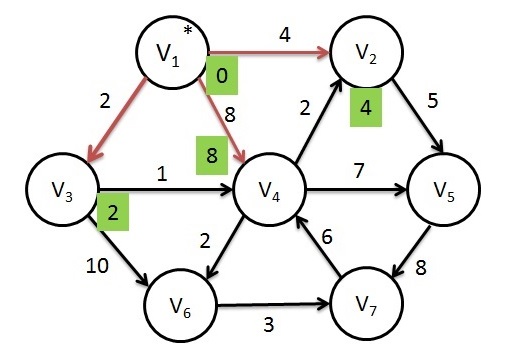
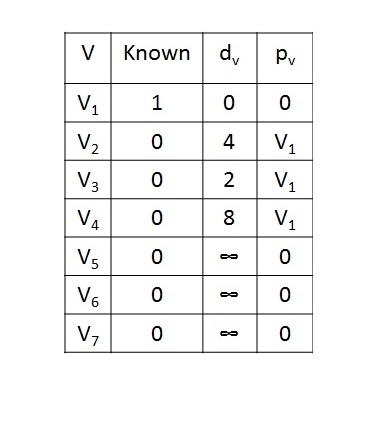
Dijkstras Algorithm - Step 2

Next, V₃ is selected and set known value to 1 and update the adjacent vertices V₄ and V₆. Actually, V₄ is already reached with cost of 8, but the cost of going through v₃ will be 3 which is smaller than the previous cost. So we can replace that old one with new distance value.

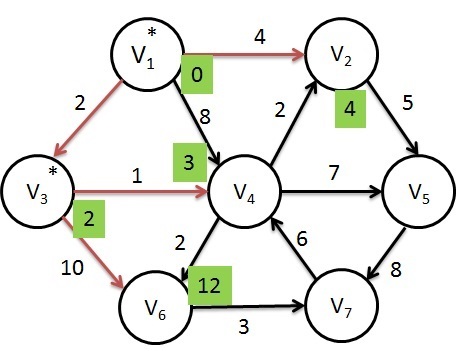
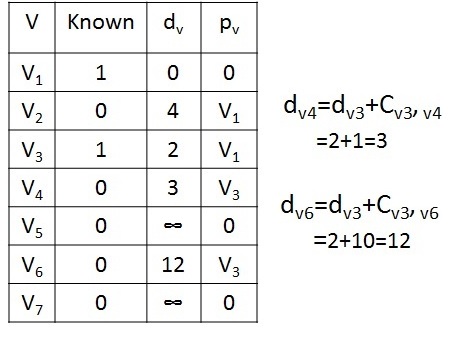
Dijkstras Algorithm - Step 3

Next, V₄ is selected and marked known. The vertices V₂, V₅ and V₆ are adjacent. The vertex V₂ is adjacent but not adjusted, because the cost of going via V₄ is 3+2=5 which is greater than the previous distance 4. So simply discards the new value. Similarly for V₆, the cost is changed to 5.

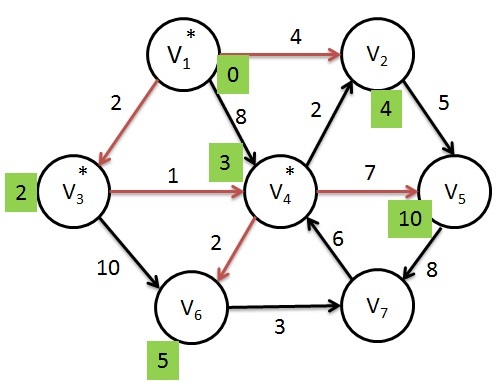
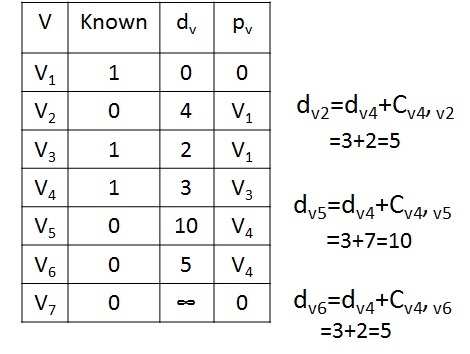
Dijkstras Algorithm - Step 4

Next, V₂ is selected and marked known. V₅ is the only adjacent vertex which is adjusted to 9(4+5) < 10.

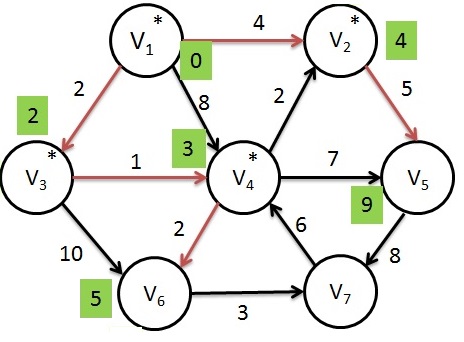
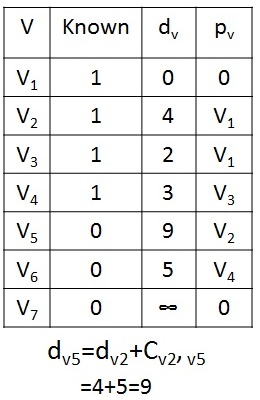
Dijkstras Algorithm - Step 5

Next, selected vertex is V₆ and marked known. V₇ is the only adjacent vertex which is adjusted to 8(5+3).

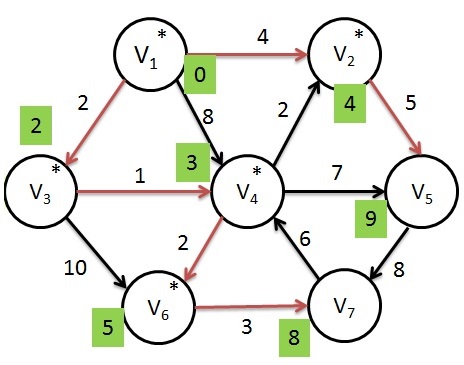
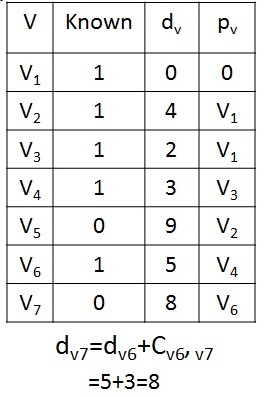
Dijkstras Algorithm - Step 6

Next, selected vertex is V₇ and set known to 1. V₄ is adjacent but already known, so no work is done on it.

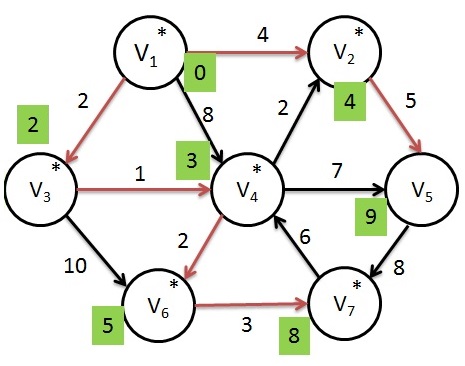
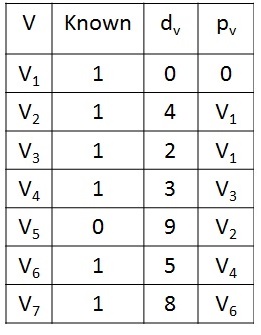
Dijkstras Algorithm - Step 7

Finally, V₅ is selected and marked known. Now the Dijkstra's algorithm is terminated and print out the shortest path from a start vertex to all other vertices.