Data Structures - Hash Table
Hash table is a data structure which stores data in an array format of fixed size. In hash table, the data is stored in the form of key / value pair. Using of hash function, it computes an index of an array where the data value to be stored. If the table size is referred to as TableSize, then the table have a range from 0 to TableSize-1 indexes in which each index is unique.
Hashing
Hashing is an implementation of hash table. It is a technique used to maps each key value into some number in the range from 0 to TableSize. It is mainly used to perform insertion, deletion and finding an element in a constant average time O(1) but it does not support any ordering such as find minimum and find maximum. There are several hash methods available such as Direct, Subtraction, Modulo division, Folding, Mid-square, Random generation etc. Here we are going to use modulo division as the hash function.
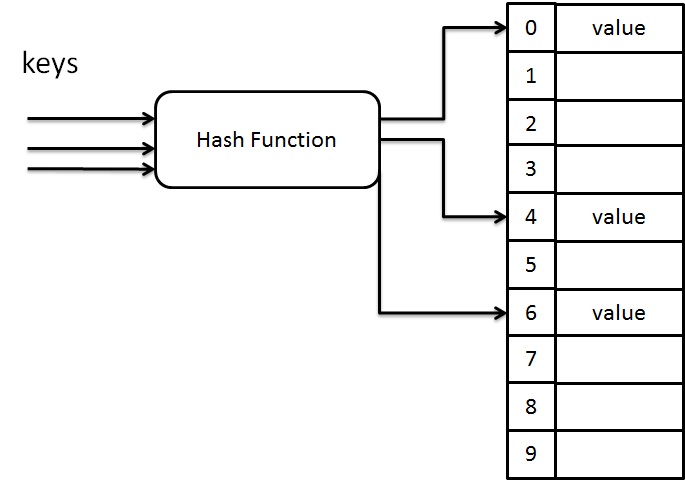
Suppose, if the inputs are integer, then the key mod TableSize gives the index in which the keys are to be placed.
Example
If the TableSize is 10 and key is 27, then
27 mod 10 = 7.
So the key 27 is placed in 7th index.
Code for Simple Hash Function
int Hash(int key,int TableSize)
{
return key % TableSize;
}Let us consider the case, if the table size is 10 and all keys end with zero, then this simple hash function is not appropriate. The reason is that, more than two keys are mapped to same index. In order to avoid this situation, we must select the table size as a prime number.
Simple Hash Function for String Input
Usually the keys are strings, so that we need to take care for choosing hash function. When the input is a string, then we add the ASCII value of each character in the string and use hash function (value mod TableSize) to get the index in which this string will be inserted.
Code For Simple Hash Function for String Input
int Hash(char *key,int TableSize)
{
int value=0;
while(*key!="\0")
value = value + *key++;
return value % TableSize;
}






