Binary Search Tree - Search, Insert, Delete. C Example Program

<<Previous - Binary Tree

Next - Expression Tree >>

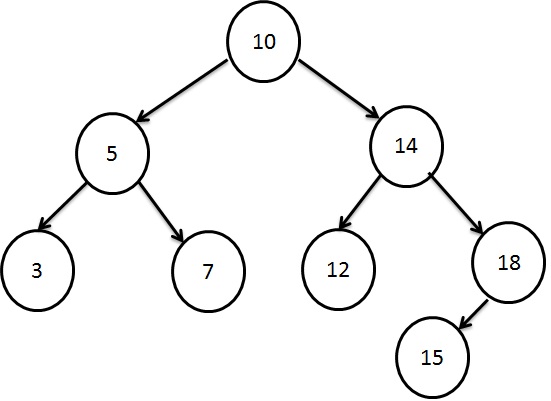
Binary Search Tree

Binary Search Tree provides a data structure with efficient insertion, deletion and search capability. Binary Search Tree is a binary tree with the following properties:

• All items in the left subtree are less than the root.
• All items in the right subtree are greater than or equal to root.
• Each subtree is itself a binary search tree

Array Vs Linked list vs Binary Search Tree

• When we store ordered data in an array structure, we can perform efficient searches but insertion and deletion are very inefficient
• When we create a linked list, we can perform efficient insertion and deletion but sequential searches are inefficient
• What we realy need is, we need a data structure that provides efficient search as well as efficient insertion and deletion capabilities

Binary Search Tree - Operations

• Search:  check the key in a tree.
• Insertion:  insert a new element into the tree.
• FindMin:  find the minimum element in the tree.
• FindMax:  find the maximum element in the tree.
• Deletion:  remove an element from the tree.

Binary Search Tree - Node Definition

Define a node contains data and its left and right children.

C Example:

  struct node
  {
    int data;
    struct node *left,*right;
  }*T;
 

Java Example:

 class Node
 {
 Object data;
 Node left,right;
 }
 

Binary Search Tree - Search Operation

• Read the value to be searched.
• Check whether the root is not null.
• If the value to be searched is less than the root, consider the left subtree for searching the particular element. Otherwise if the value is greater than the root, consider the right subtree to search the particular element.
• If the value is present in the tree then return the position of that searched value.

struct node *search(int data, struct node *T)
  {
    if (T==NULL)
     return NULL;
	else
    {
       if (T->data!= data)
        {
           if(T->data<data)
             {
               T=T->left;
               return search(data,T);
             }
           else
             {
                T=T->right;
                return search(data,T);
             }
        }
       else
         return T;
    }
  }

Binary Search Tree - Find Minimum operation

• Returns the position of the smallest element in the tree.
• To perform this, start at the root and go left as long as there is a left child.
• The stopping end is the smallest element.

 struct node *findMin(struct node *T)
  {
    if(T==NULL)
       return NULL;
    else
      if(T->left==NULL)
         return T;
     else
       return findMin(T->left);
  }
 

Binary Search Tree - Find Maximum

• Returns the position of the largest element in the tree.
• To perform this, start at the root and go right as long as there is a right child.
• The stopping end is the largest element.

 struct node *findMax(struct node *T)
 {
   if(T==NULL)
      return NULL;
   else
    if(T->right==NULL)
      return T;
    else
      return  findMax(T->right);
  }

Binary Search Tree - Insertion Operation

• Read the value to be inserted.
• First perform the search operation to check whether the key values is different from those existing element.
• If the search is unsuccessful, then the key is inserted at the point the search is terminated.

struct node *insert(int element,struct node *T)
{
	if(T==NULL)
	{
	 T=(struct node*)malloc(sizeof(struct node));
	   if(T==NULL)
		printf("no memory\n");
	   else
	    {
	     T->data = element;
	     T->right = T->left = NULL;
	    }
       }
     else if(element< = T->data)
	    T->left = insert(element,T->left);
     else if(element> = T->data)
	    T->right = insert(element,T->right);
     return T;
  }

Binary Search Tree - Deletion Operation

• Read the key value to be deleted.
• First perform search operation to get that particular key element.
• If it is, check whether
  1. it is leaf node,
  2. or it has only one sub-tree
  3. or it has exactly 2 sub-trees.
• If the key value is the leaf-node, assign null value to that node .
• Else if the key contains only one sub-tree either left (or)right sub-tree, if the key is root, it is discarded and the root its single sub-tree becomes the new search tree root. Else if the key is the child node, then we change the pointer from the root of key to the child of the key.
• If the key contain both left and right sub-tree replace the key with either largest element is the left sub-tree or smallest element is the right sub-tree.

struct node *delete(int data,struct node *T)
{
  struct node *temp;
   if(T==NULL)
   	printf("no element\n");
   else if(data<T->data)
   	return delete(data,T->left);
   else if(data>T->data)
	return delete(data,t->right);
   else
     if(T->left && T->right)
      {
        temp=findmin(T->right);
        T->data=temp->data;
        return delete(T->data,T->right);
      }
     else
       {
         temp=T;
         if(T->left==NULL)
	       T=T->right;
         else if(T->right==NULL)
	       T=T->left;
           free(temp);
        }
     return T;
 }

<< Previous - Binary Tree

Next - Expression Tree >>