Shortest Path Algorithms
Shortest Path Algorithms
For a given graph, the shortest path algorithms determine the minimum cost of the path from source vertex to every vertex in a graph.
Path is the movement traced across sequence of vertices V1, V2, V3,....,VN in a graph. Cost of the path is the sum of the cost associated with all the edges in a graph. This is represented as:
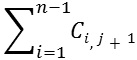
- If the graph is weighted, then the cost of the path is the sum of weights on its edges.
- If the graph is not weighted, the cost of the path is the number of edges on the path.
Where does the shortest path algorithm find its applications?
- We can use the shortest path algorithm to find the cheapest way to send the information from one computer to another within a network.
- We can use the shortest path algorithm to find the best route between the two airports.
- We can use to find a road route which requires minimum distance from a starting source to an ending destination. We can determine the route which requires minimum time to an ending destination
Shortest path Problems
- There are different kinds of shortest-path problems.
- The single source shortest path problemis used to find minimum cost from single source to all other vertices.
- The all-pairs shortest path problemis used to find the shortest path between all pairs of vertices.
- The single source shortest path problem is solved by using Dijkstra's algorithm and the all-pairs shortest-path problem is solved by using Floyd-Warshall Algorithm. Let us look at Dijkstra's algorithm.









