Hashing Collision Resolution - Linear Probing
Linear Probing
Linear Probing is one of the 3 open addressing / closed hashing collision resolution techniques
This is a simple method, sequentially tries the new location until an empty location is found in the table.
For example: inserting the keys {79, 28, 39, 68, 89} into closed hash table by using same function and collision resolution technique as mentioned before and the table size is 10 ( for easy undestanding we are not using prime number for table size). The hash function is hi(X) = ( Hash(X) + F(i)) % TableSize for i = 0, 1, 2, 3,...etc.
Solution:
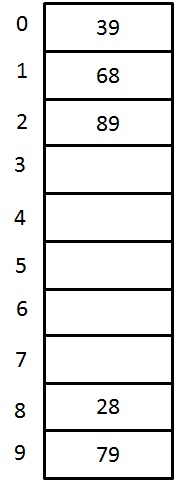
| Key | Hash Function h(X) | Index | Collision | Alt Index |
|---|---|---|---|---|
| 79 | h0(79) = (Hash(79)+F(0))%10 = ((79%10)+0)%10 = 9 | 9 | ||
| 28 | h0(28) = (Hash(28)+F(0))%10 = ((28%10)+0)%10 = 8 | 8 | ||
| 39 | h0(39) = (Hash(39)+F(0))%10 = ((39%10)+0)%10 = 9 | 9 | first collision occurs | |
| h1(39) = (Hash(39)+F(1))%10 = ((39%10)+1)%10 = 0 | 0 | 0 | ||
| 68 | h0(68) = (Hash(68)+F(0))%10 = ((68%10)+0)%10 = 8 | 8 | collision occurs | |
| h1(68) = (Hash(68)+F(1))%10 = ((68%10)+1)%10 = 9 | 9 | Again collision occurs | ||
| h2(68) = (Hash(68)+F(2))%10 = ((68%10)+2)%10 = 0 | 0 | Again collision occurs | ||
| h3(68) = (Hash(68)+F(3))%10 = ((68%10)+3)%10 = 1 | 1 | 1 | ||
| 89 | h0(89) = (Hash(89)+F(0))%10 = ((89%10)+0)%10 = 9 | 9 | collision occurs | |
| h1(89) = (Hash(89)+F(1))%10 = ((89%10)+1)%10 = 0 | 0 | Again collision occurs | ||
| h2(89) = (Hash(89)+F(2))%10 = ((89%10)+2)%10 = 1 | 1 | Again collision occurs | ||
| h3(89) = (Hash(89)+F(3))%10 = ((89%10)+3)%10 = 2 | 2 | 2 |
The problem with linear probing is primary clustering. This means that even if the table is empty, any key that hashes to table requires several attempt to resolve the collision because it has to cross over the blocks of occupied cell. These blocks of occupied cell form the primary clustering. If any key falls into clustering, then we cannot predict the number of attempts needed to resolve the collision. These long paths affect the performance of the hash table.







