Hashing Collision avoidance - Quadratic Probing
Quadratic Probing
Quadratic probing is an open addressing method for resolving collision in the hash table. This method is used to eliminate the primary clustering problem of linear probing. This technique works by considering of original hash index and adding successive value of an arbitrary quadratic polynomial until the empty location is found. In linear probing, we would use H+0, H+1, H+2, H+3,.....H+K hash function sequence. Instead of using this sequence, the quadratic probing would use the another sequence is that H+12, H+22, H+32,....H+K2. Therefore, the hash function for quadratic probing is
hi(X) = ( Hash(X) + F(i)2) % TableSize for i = 0, 1, 2, 3,...etc.
Let us examine the same example that is given in linear probing:
Solution:
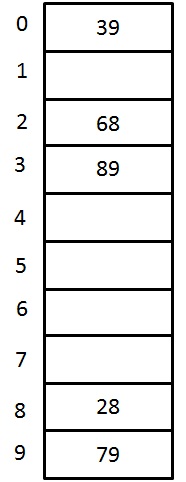
| Key | Hash Function h(X) | Index | Collision | Alt Index |
|---|---|---|---|---|
| 79 | h0(79) = ( Hash(79) + F(0)2) % 10 = ((79 % 10) + 0) % 10 | 9 | ||
| 28 | h0(28) = ( Hash(28) + F(0)2) % 10 = ((28 % 10) + 0) % 10 | 8 | ||
| 39 | h0(39) = ( Hash(39) + F(0)2) % 10 = ((39 % 10) + 0) % 10 | 9 | The first collision occurs | |
| h1(39) = ( Hash(39) + F(1)2) % 10 = ((39 % 10) + 1) % 10 | 0 | 0 | ||
| 68 | h0(68) = ( Hash(68) + F(0)2) % 10 = ((68 % 10) + 0) % 10 | 8 | The collision occurs | |
| h1(68) = ( Hash(68) + F(1)2) % 10 = ((68 % 10) + 1) % 10 | 9 | Again collision occurs | ||
| h2(68) = ( Hash(68) + F(2)2) % 10 = ((68 % 10) + 4) % 10 | 2 | 2 | ||
| 89 | h0(89) = ( Hash(89) + F(0)2) % 10 = ((89 % 10) + 0) % 10 | 9 | The collision occurs | |
| h1(89) = ( Hash(89) + F(1)2) % 10 = ((89 % 10) + 1) % 10 | 0 | Again collision occurs | ||
| h2(89) = ( Hash(89) + F(2)2) % 10 = ((89 % 10) + 4) % 10 | 3 | 3 |
Although, the quadratic probing eliminates the primary clustering, it still has the problem. When two keys hash to the same location, they will probe to the same alternative location. This may cause secondary clustering. In order to avoid this secondary clustering, double hashing method is created where we use extra multiplications and divisions







