Graph - Adjacency Matrix Representation

<<Previous - Degree of Graph

Next - Graph Adjacency List >>

In this page, we will learn about Adjacency Matrix Representation of graph.

Graph Representation

There are different ways to represent Graph - Adjacency Matrix Representation & Adjacency List Representation

Adjacency Matrix Representation

One simple way is to use adjacency matrix representation which uses a two-dimensional array. Adjacency matrix is a square matrix with each entry indicating whether a pair of vertices are adjacent to each another.

• If there is an edge between two vertices v_i and v_j, then we set A[v_i][v_j]=1.
• Otherwise we set the entry in the array to 0.

  

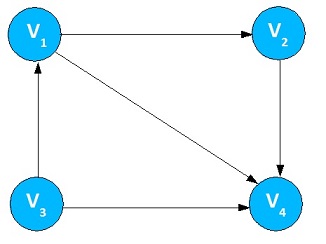
  For the above graph, For adjacency matrix, put 1 in the table as shown below if V_i and V_j have edge in the graph else put 0.

  

  
  
  

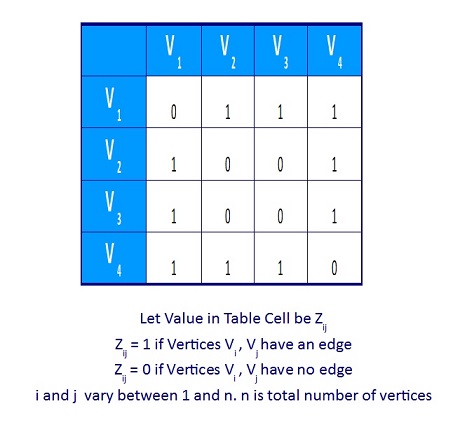
  Suppose, if the edge is associated with weight, then we can set A[v_i][v_j] equal to the weight. The memory space required for this adjacency matrix is O(|V|²).

  
  

  

  

  
  
  

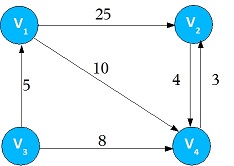
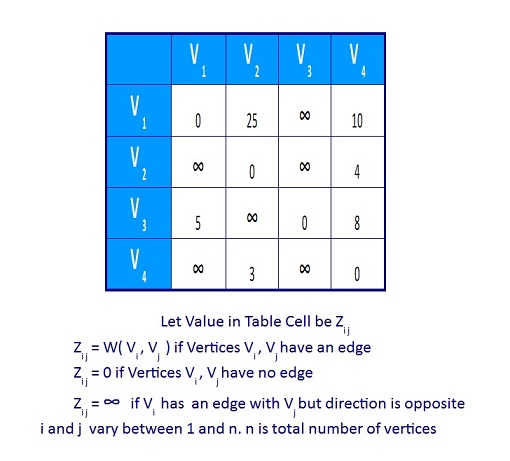
  For adjacency matrix, put the weightage in the table if V_i and V_j have edge with weightage, else put some constant C. Here we take the constant as ∞.The self ending edge weightage is 0. If the graph is dense, an adjacency matrix is suitable for graph representation.

  ---

  << Previous - Degree of Graph

  Next - Graph Adjacency List >>

  
  
  

  ---