Infix Traversal to Produce Expression from Expression Tree
<< Previous - Postfix Expression Tree
Expression Tree is used to represent expressions. Let us look at how to traverse an expression tree to produce an infix expression from expression tree:
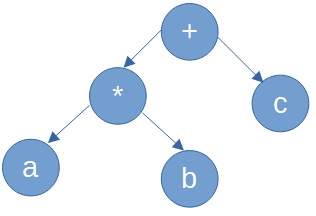
Steps to Traverse Expression Tree to produce Infix Expression for a*b+c
Infix traversal of expression tree involves traversing
- the left subtree,
- then the root node and
- then the right subtree.
Traverse Expression Tree to produce Infix Expression
Let us how to traverse expression tree and form an Infix expression. An infix expression is generated from the tree as follows:
- First consider the left subtree a * b.
- For a * b, consider the left subtree a. Left subtree has only one node a, Hence, first write the same.
Infix expression created so far = a
- Consider the root of subtree *.
Infix expression created so far = a *
- Consider the right subtree. right subtree b is just a node.
Infix expression created so far = a * b
- For a * b, consider the left subtree a. Left subtree has only one node a, Hence, first write the same.
- Consider the root + .
Infix expression created so far = a * b +
- Consider the right subtree c . Since the right subtree is just a simple node, there is no more subtrees to be checked
Infix expression created so far = a * b + c
How to write Prefix Expression >>
How to write Postfix Expression >>
<< Previous - Postfix Expression Tree






